Sonstiges

Und Ihr meckert über meine Rechenaufgabe

23. Okt 2008

dann löst mal dieses Kommentar-Captcha:
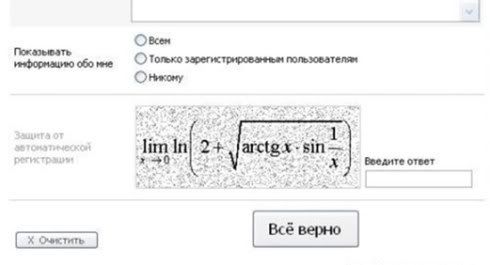
captcha-135
Lösung auf info-tain melden.

Unsere Empfehlungen für dich

Über den Autor

Robert Basic

Robert Basic ist Namensgeber und Gründer von BASIC thinking und hat die Seite 2009 abgegeben. Von 2004 bis 2009 hat er über 12.000 Artikel hier veröffentlicht.

Zu allen Artikeln

27 Kommentare

  • Ohne jetzt mein Mathebuch zu konsultieren, und nach etlichen Jahren ohne Logarithmen und Grenzwertberechnungen würde ich vermuten, daß das Captcha nicht lösbar ist.

    sin 1/x wird beim Einsetzen der 0 zu sin 1/0. Durch 0 kann man nicht teilen, daher ist der Inhalt der Wurzel nicht lösbar.

  • @Andy: da steht nicht x=0 sondern x tendiert zu null und damit ist x ungleich 0.
    @Robert: Trau Dich doch und bau den Captcha hier ein, hehehe.

    *mitdemzeigefingeraufrobertzeigundsing*
    „Du traust dich nicht, du traust dich nicht! nänänänänäää nä!“

  • Ich finde deine Rechenaufgaben schon schwer genug, weil bei dir die Zahlen ausgeschrieben werden. 😉

    Vielen Dank für den Backlink, Robert!

  • Wenn man sich nicht im Klaren ist, was da passiert, kann man das ja einfach mal in Excel eintippen: =LN(2+WURZEL(ARCTAN(B1)*SIN(1/B1))) Um das ganze weiter aufzudröseln, kann man sich auch noch die einzelnen Terme ansehen, was die so machen, wenn B1 immer kleiner wird. Aber nicht für B1 Null einsetzen. Das funktioniert nicht.
    Es ergibt sich dann das Problem, dass der Term unter der Wurzel irgendwann das erste Mal negativ wird. Und dann kann man die Wurzel nimmer ziehen. Wird der Wert für B1 noch kleiner, wird der Term unter der Wurzel irgendwann wieder positiv. Und so geht das lustig weiter.

    Eine weitere Möglichkeit ist, sich die Terme einzeln als Graphen anzusehen.
    Da sieht man, dass der Arcustangens bei 0 einen Nulldurchgang hat, also keine Probleme macht. Anders sieht das bei sin (1/x) aus, weil x nicht null werden darf, ist der Wert selbst nicht definiert. Der Sinus hat aber bei 0 einen Nulldurchgang. Daher müsste der Grenzwert der Funktion sin (1/x) gegen 0 ebenfalls bei 0 liegen. Dann würde der Wert unter der Wurzel ganz klein, so dass ln2 das Ergebnis sein dürfte, so wie Michael #3 schon geschrieben hat. Das Ergebnis wäre dann 0,693…

    Oder..?

    Edit @#10: Das hättest du auch etwas früher posten können… 😉

  • Ich bin auch ganz klar für ln(2).

    Wobei auch eine Negative Wurzel kein Problem wär.

    Dann ist das Ergebnis halt Komplex.

  • also ich kann wenigstens das lesen was da steht (als ossitusse) ;o) das eine konnte ich sogar noch verstehen: pokasuiwatsch informatznju obo mnje… mann ist das lange her… :o)

  • @ Will Sagen:

    sin(1/x) geht nicht gegen Null, sondern sein Grenzwert ist nicht definiert. Einfach ausgedrückt, da der Sinus zwischen -1 und 1 schwankt.

    Gruß Michael

  • Naja, ok. Ich habe versucht, es vielleicht für ein paar Leute verständlich(er) zu erklären. Da habe ich leider daneben gelegen.

    Verstehe ich das dann richtig, dass sin (1/x) quasi um 0 „herumspringt“? Weil der Wert aber so klein ist, hat er auf das Ergebnis keinen entscheidenden Einfluss, so das ln2 herauskommt?

  • @WillSagen: Ich denke, dass arctan(0) = 0. Deshalb spielt der sin keine Rolle.

    Der sin(1/x) mit lim -> 0 alterniert. Das Argument des sin (1/X) wird fast unendlich groß. Der Sinus nimmt im unendlichen ja immer noch Werte zwischen -1 und 1 an. Welchen davon kann man nicht sagen, denke ich mal.

  • Jau, besten Dank für den Nachhilfeunterricht. Ist eben alles schon verdammt lange her. 😉 Dafür gar nicht so schlecht, finde ich 🙂
    @#19 Eines habe ich nicht verstanden: Es geht ja nicht um den Grenzwert für x gegen unendlich, sondern gegen Null. Ändert das was?

    Edit: Halt, stop. Hab nicht richtig gelesen. Hat sich geklärt.

  • Was willst du mit der Handcreme, sprich? *kalauer rausholt*

    Ich denke auch, dass die Lösung ln(2) bzw. 0,69…. ist. Alles andere würde meinem mathematischen Verständnis wiedersprechen.

  • Ich stimme #2 Andy zu, ich habe zwar noch nicht sin gemacht in der Schule, aber gelernt, dass durch 0 nicht teilbar ist.
    und da am anfang der gleichung x -> 0 steht, ist dies nicht machbar.

  • Das ist gerade der Witz bei Grenzwertbetrachtungen. Man nähert sich dem Grenzwert, ohne ihn selbst in die Berechnung einzusetzen. x ist daher nie genau null, und darum kann man den Quotient 1/x doch bilden.
    Das kommt noch früh genug in der Schule…

  • Hi@all
    ich glaub ich werd langsam verrückt^^
    da hock ich den ganzen tag in der schule und muss mir so zeug anhören und dann will ich abends entspannen und was muss ich da lesen…. Oo
    xD
    btw: großes lob an dich, robert, dein blog is echt toll!